Co-rotating vortices#
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import animation
plt.rcParams['figure.figsize'] = (10,6)
%config InlineBackend.figure_format = 'retina'
import sys
if sys.platform == "darwin":
%env CC=gcc-10
%load_ext fortranmagic
%%fortran --f90flags "-fopenmp" --extra "-lgomp"
subroutine biot ( n, xp, yp, op, up, vp )
implicit none
integer, intent(in) :: n
real(8), intent(in) :: xp( n ), yp( n ), op( n )
real(8), intent(out) :: up( n ), vp( n )
!f2py optional , depend(a) :: n=len(xp)
integer :: k, j
real(8) :: dpi, a1, a12, a122, r2, r22, r2a1, r2a13
real(8) :: f_ik, usum, vsum, dx, dy
dpi = 8d0 * atan( 1d0 )
a1 = .05
a12 = a1*a1
a122 = a12*a12
!$OMP PARALLEL DO DEFAULT(FIRSTPRIVATE) SHARED(up, vp)
do k = 1, n
usum = 0
vsum = 0
do j = 1, n
dx = xp( j ) - xp( k )
dy = yp( j ) - yp( k )
r2 = dx * dx + dy * dy
if ( r2 > 1e-12 ) then
r22 = r2 * r2
r2a1 = r2 + a12
r2a13 = r2a1 * r2a1 * r2a1
f_ik = ( r22 + 3d0*a12*r2 + 4d0*a122 ) / r2a13
usum = usum + dy * op(j) * f_ik
vsum = vsum - dx * op(j) * f_ik
end if
end do
up(k) = usum / dpi
vp(k) = vsum / dpi
end do
!$OMP END PARALLEL DO
end subroutine biot
def distrib(ray, nray = 10, nsec = 6, gauss=True, gam0 = 1.0, eps= 0):
"""
Particles distributed evenly spaced into a disc.
rf,zf : particles positions
ds : particle surface size
cir : particle circulation
dr : size step along radial axis
nray : nb of points along adial axis
dray : particle ray in the center
ray : disc ray
gam0 : total strength of the vortex
surf : disc surface
nsec : number of particles around the center particle
eps : ellipsis parameter
"""
pi = np.pi
dr = ray / (nray + 0.5)
dray = 0.5 * dr
surf = pi * ray * ray
dtheta = 2.0 * pi / nsec
k = 0
rf = [0.0]
zf = [0.0]
ds = [pi * dray * dray]
if gauss:
gamt = gam0 / (1. - np.exp(-1.0))
cf = [gamt * (1. - np.exp(-(dray / ray) ** 2))] # gaussian
else:
cf = [gam0 * ds[k] / surf] # uniform
r1 = dray
s1 = pi * r1 ** 2
nsec0 = nsec
nsec = 0
for i in range(nray):
nsec = nsec + nsec0
dtheta = 2.0 * pi / nsec
r = (i + 1) * dr
r2 = r + 0.5 * dr
s2 = pi * r2 ** 2
dss = s2 - s1
s1 = s2
for j in range(nsec):
k = k + 1
theta = (j + 1) * dtheta
sigma = r * (1.0 + eps * np.cos(2.0 * theta))
rf.append(sigma * np.cos(theta))
zf.append(sigma * np.sin(theta))
ds.append(dss / nsec)
if gauss: # gaussian
q = 0.5 * (np.exp(-(r1 / ray) ** 2) - np.exp(-(r2 / ray) ** 2))
strength = gamt * dtheta / pi * q
else: # uniform
strength = gam0 * ds[k] / surf
cf.append(strength)
r1 = r2
kd = k - nsec + 1
nr = k
print (len(rf),len(zf),len(cf))
ssurf = np.sum(ds)
sgam = np.sum(cf)
print('toal number of particles :', nr)
print('check surface :', (surf), ' - ', (ssurf))
if (gauss):
print('check vortex strength :', (gam0), ' ; ', (sgam))
else:
print('check vortex strength :', (gam0), ' ; ', (sgam))
return np.array(rf), np.array(zf), np.array(ds), np.array(cf)
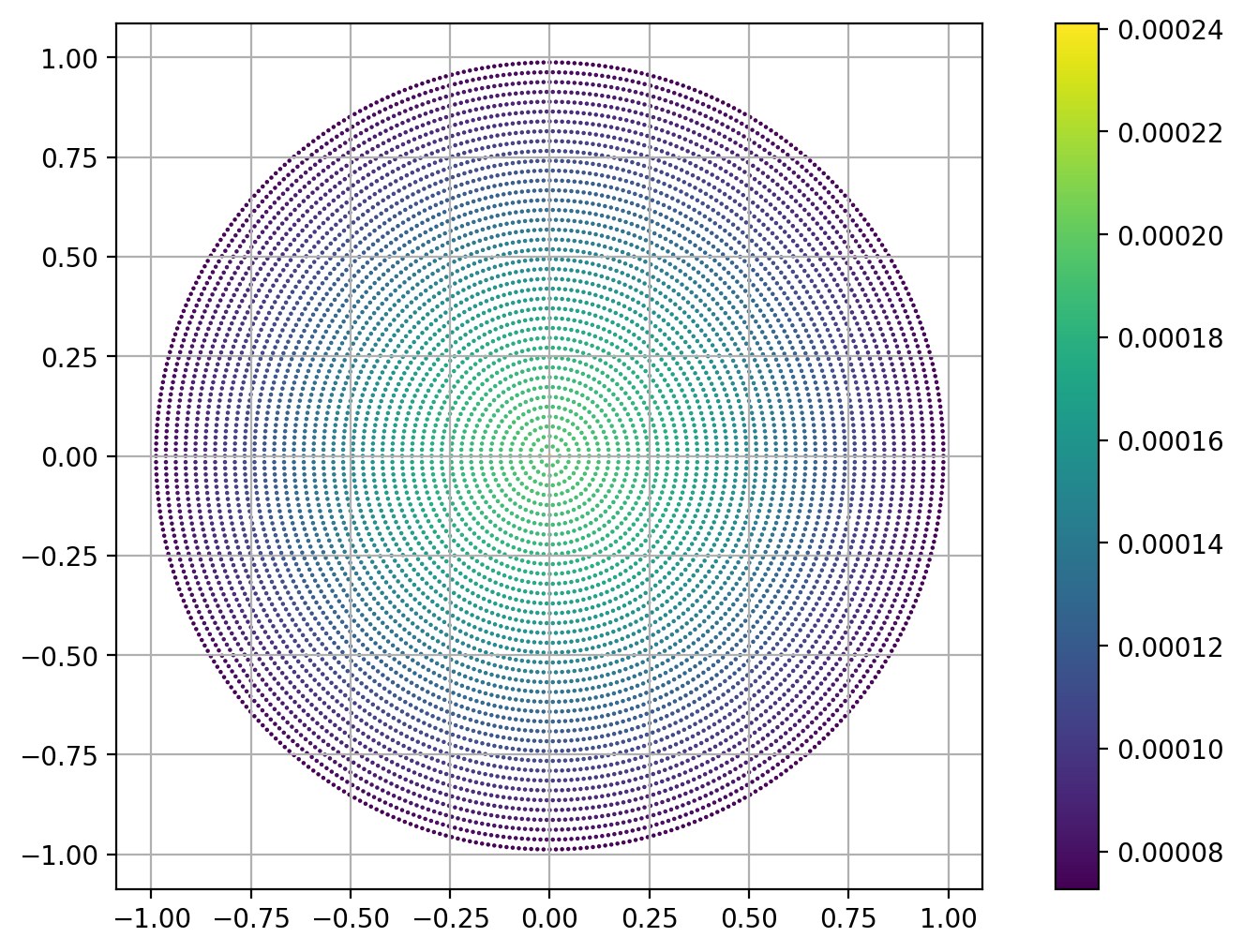
r, z, s, g = distrib(1.0,nray = 40,nsec = 10)
plt.scatter(r, z, 1e3*s, g)
plt.axis('scaled')
plt.grid(True)
plt.colorbar();
8201 8201 8201
toal number of particles : 8200
check surface : 3.141592653589793 - 3.141592653589793
check vortex strength : 1.0 ; 1.0
nstep = 1
amach = 0.1
nproc = 1
dt = 0.1
pi = np.pi
r0 = 0.6
u0 = amach
#gam0 = u0 * 2.0 * pi / 0.7 * r0 !gaussienne
#gam0 = 2. * pi * r0 * u0 !constant
gam0 = 2. * pi / 10.0
aom = gam0 / ( pi * r0**2 ) #Amplitude du vortex
tau = 8.0 * pi**2 / gam0 #Periode de co-rotation
gomeg = gam0/ (4.0*pi) #Vitesse angulaire
print( " --------------------------------------------- ")
print( " steps : ", nstep)
print( " time step : ", dt)
print( " aom = ", aom)
print( " r0 = ", r0)
print( " strength = ", gam0)
print( " rotation speed gomeg = ", gomeg)
print( " corotation period = ", tau)
print( " --------------------------------------------- ")
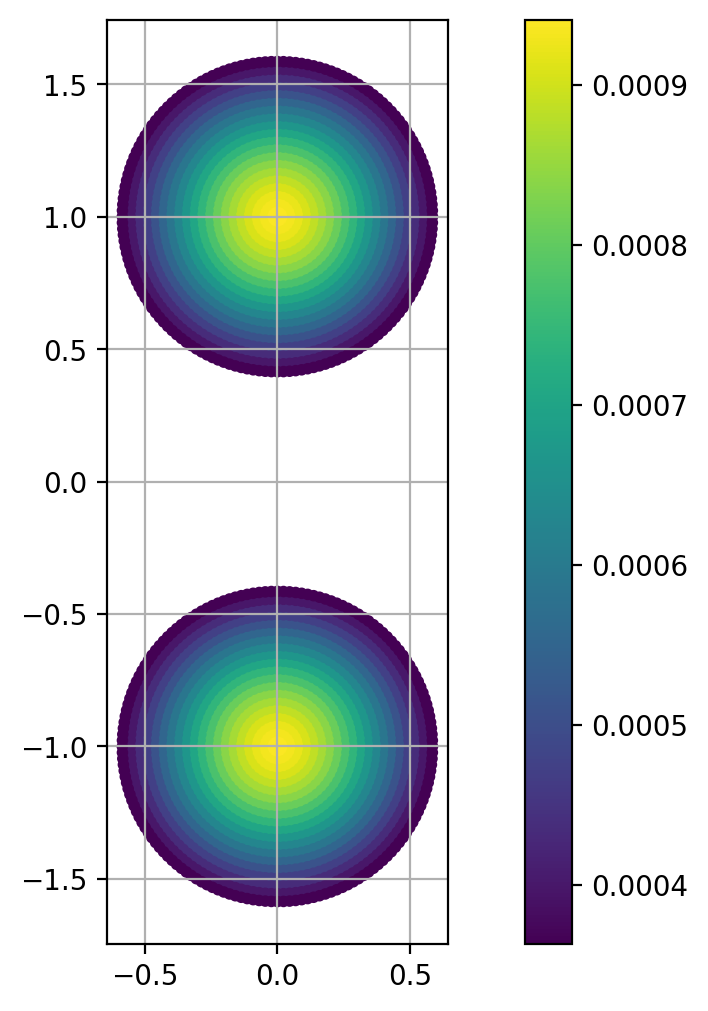
rf, zf , ds, gam = distrib( r0, nray = 20, nsec = 8 )
n = 2 * rf.size
X = np.zeros((n,2),dtype=np.float64)
X[:,0] = np.concatenate([rf, rf])
X[:,1] = np.concatenate([zf + 1., zf - 1])
op = np.concatenate([gam,gam])
---------------------------------------------
steps : 1
time step : 0.1
aom = 0.5555555555555556
r0 = 0.6
strength = 0.6283185307179586
rotation speed gomeg = 0.05
corotation period = 125.66370614359172
---------------------------------------------
1681 1681 1681
toal number of particles : 1680
check surface : 1.1309733552923256 - 1.1309733552923256
check vortex strength : 1.0 ; 0.9999999999999999
n = X.shape[0]
plt.scatter(X[:,0], X[:,1], 10*np.ones(n), op)
plt.axis('scaled')
plt.grid(True)
plt.colorbar();
fig = plt.figure()
fig.subplots_adjust(left=0, right=1, bottom=0, top=1)
ax = fig.add_subplot(111, aspect='equal', autoscale_on=False,
xlim=(-2, 2), ylim=(-2, 2));
# particles holds the locations of the particles
particles, = ax.plot([], [], 'bo', ms=2);
def init():
particles.set_data([], [])
return particles,
def animate(i):
global dt, ax, fig, X
up, vp = biot(X[:,0], X[:,1], op)
up, vp = biot(X[:,0] + 0.5 * dt * up,
X[:,1] + 0.5 * dt * vp, op)
X[:,0] += dt * up
X[:,1] += dt * vp
particles.set_data(X[:, 0], X[:, 1])
return particles,
ani = animation.FuncAnimation(fig, animate, frames=400,
interval=10, blit=True, init_func=init);
from IPython.display import HTML
HTML(ani.to_jshtml())
Animation size has reached 21000370 bytes, exceeding the limit of 20971520.0. If you're sure you want a larger animation embedded, set the animation.embed_limit rc parameter to a larger value (in MB). This and further frames will be dropped.