Maxwell solver in two dimensions with FDTD scheme¶
\[
\frac{\partial H_z}{\partial t} = \frac{\partial E_x}{\partial y} - \frac{\partial E_y}{\partial x}
;\qquad
\frac{\partial E_x}{\partial t} = \frac{\partial H_z}{\partial y}
;\qquad
\frac{\partial E_y}{\partial t} = - \frac{\partial H_z}{\partial x}
\]
\[
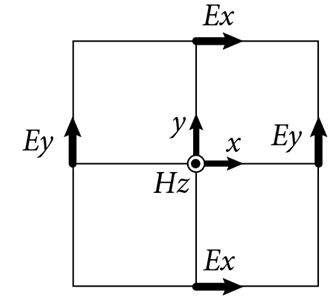
H_z \big|^{n+1/2}_{i+1/2,j+1/2} = H_z \big|^{n-1/2}_{i+1/2,j+1/2} +
\frac{dt}{dy} \big(E_x \big|^{n}_{i+1/2,j+1} - E_x \big|^{n}_{i+1/2,j} \big)
- \frac{dt}{dx} \big( E_y \big|^{n}_{i+1,j+1/2} - E_y \big|^{n}_{i,j+1/2} \big)
\]
\[
E_x \big|^{n+1}_{i+1/2,j} = E_x \big|^{n}_{i+1/2,j} + \frac{dt}{dy} \big( H_z \big|^{n+1/2}_{i+1/2,j+1/2} - H_z \big|^{n+1/2}_{i-1/2, j-1/2} \big)
\]
\[
E_y \big|^{n+1}_{i,j+1/2} = E_y \big|^{n}_{i,j+1/2} - \frac{dt}{dx} \big( H_z \big|^{n+1/2}_{i+1/2,j+1/2} - H_z \big|^{n+1/2}_{i-1/2, j+1/2} \big)
\]
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import axes3d
import matplotlib.animation as animation
from IPython.display import HTML
plt.rcParams['figure.figsize'] = (10,6)
# Mesh parameters
nx, ny = 101, 101
vx, dx = np.linspace(0, 1, nx, endpoint=True, retstep=True)
vy, dy = np.linspace(0, 1, ny, endpoint=True, retstep=True)
#Initialize Ex, Ey when time = 0
ex = np.zeros((nx-1, ny), dtype=np.double)
ey = np.zeros((nx, ny-1), dtype=np.double)
nbiter = 500 # time loop size
dt = 0.001 # time step
m, n = 2, 2
omega = np.sqrt((m*np.pi)**2+(n*np.pi)**2)
# Create the staggered grid for Bz
x, y = np.meshgrid(0.5*(vx[:-1]+vx[1:]), 0.5*(vy[:-1]+vy[1:]))
fig = plt.figure()
ax = axes3d.Axes3D(fig)
#Initialize Bz when time = - dt / 2
hz = - np.cos(m*np.pi*y) * np.cos(n*np.pi*x) * np.cos(omega*(-0.5*dt))
wframe = ax.plot_wireframe(x, y, hz, rstride=2, cstride=2)
ax.set_zlim(-1,1);
/var/folders/24/8k48jl6d249_n_qfxwsl6xvm0000gn/T/ipykernel_27776/2363328554.py:2: MatplotlibDeprecationWarning: Axes3D(fig) adding itself to the figure is deprecated since 3.4. Pass the keyword argument auto_add_to_figure=False and use fig.add_axes(ax) to suppress this warning. The default value of auto_add_to_figure will change to False in mpl3.5 and True values will no longer work in 3.6. This is consistent with other Axes classes.
ax = axes3d.Axes3D(fig)
numpy¶
def faraday( ex, ey, hz ) :
"faraday equation Bz(t+dt/2) -> Bz(t-dt/2) + dt f(E(t))"
return hz + dt * ((ex[:, 1:]-ex[:, :-1]) / dy - (ey[1:, :]-ey[:-1, :]) / dx)
def ampere_maxwell( hz, ex, ey):
" Ampere-Maxwell equation E(t+dt) -> E(t) + dt g(Bz(t+dt/2)) "
ex[:, 1:-1] += dt*(hz[:, 1:]-hz[:, :-1]) / dy
ey[1:-1, :] += - dt*(hz[1:, :]-hz[:-1, :]) / dx
# periodic boundary conditions
ex[:, 0] += dt*(hz[:, 0]-hz[:, -1]) / dy
ex[:, -1] = ex[:, 0]
ey[0, :] += - dt*(hz[0, :]-hz[-1, :]) / dx
ey[-1, :] = ey[0, :]
return ex, ey
def update(i, ax, fig):
ax.cla()
global ex, ey, hz
for j in range(10):
hz = faraday( ex, ey, hz)
ex, ey = ampere_maxwell( hz, ex, ey)
wframe = ax.plot_wireframe(x, y, hz, rstride=2, cstride=2)
ax.set_zlim(-1, 1)
return wframe,
ani = animation.FuncAnimation(fig, update,
frames=range(100),
fargs=(ax, fig), interval=20, blit=True)
%%time
HTML(ani.to_html5_video())
CPU times: user 14.8 s, sys: 328 ms, total: 15.1 s
Wall time: 20.5 s
%%time
from tqdm.notebook import tqdm
nx, ny = 512, 512
vx, dx = np.linspace(0, 1, nx, endpoint=True, retstep=True)
vy, dy = np.linspace(0, 1, ny, endpoint=True, retstep=True)
ex = np.zeros((nx-1, ny), dtype=np.double)
ey = np.zeros((nx, ny-1), dtype=np.double)
dt = 0.001 # time step
m, n = 2, 2
omega = np.sqrt((m*np.pi)**2+(n*np.pi)**2)
x, y = np.meshgrid(0.5*(vx[:-1]+vx[1:]), 0.5*(vy[:-1]+vy[1:]))
hz = - np.cos(m*np.pi*y) * np.cos(n*np.pi*x) * np.cos(omega*(-0.5*dt))
for t in tqdm(range(1000)):
hz = faraday( ex, ey, hz)
ex, ey = ampere_maxwell( hz, ex, ey)
CPU times: user 5.16 s, sys: 86 ms, total: 5.25 s
Wall time: 5.22 s
%load_ext fortranmagic
fortran¶
%%fortran
subroutine faraday_fortran( ex, ey, bz, dx, dy, dt, nx, ny)
implicit none
real(8), intent(in) :: ex(nx-1,ny)
real(8), intent(in) :: ey(nx,ny-1)
real(8), intent(inout) :: bz(nx-1,ny-1)
integer, intent(in) :: nx, ny
real(8), intent(in) :: dx, dy, dt
integer :: i, j
real(8) :: dex_dx, dey_dy
real(8) :: dex_dy, dey_dx
do j=1,ny-1
do i=1,nx-1
dex_dy = (ex(i,j+1)-ex(i,j)) / dy
dey_dx = (ey(i+1,j)-ey(i,j)) / dx
bz(i,j) = bz(i,j) + dt * (dex_dy - dey_dx)
end do
end do
end subroutine faraday_fortran
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
/var/folders/24/8k48jl6d249_n_qfxwsl6xvm0000gn/T/ipykernel_27776/744418150.py in <module>
----> 1 get_ipython().run_cell_magic('fortran', '', '\nsubroutine faraday_fortran( ex, ey, bz, dx, dy, dt, nx, ny)\nimplicit none\n\nreal(8), intent(in) :: ex(nx-1,ny)\nreal(8), intent(in) :: ey(nx,ny-1)\nreal(8), intent(inout) :: bz(nx-1,ny-1)\ninteger, intent(in) :: nx, ny\nreal(8), intent(in) :: dx, dy, dt\n\ninteger :: i, j\nreal(8) :: dex_dx, dey_dy\nreal(8) :: dex_dy, dey_dx\n \ndo j=1,ny-1\ndo i=1,nx-1\n dex_dy = (ex(i,j+1)-ex(i,j)) / dy\n dey_dx = (ey(i+1,j)-ey(i,j)) / dx\n bz(i,j) = bz(i,j) + dt * (dex_dy - dey_dx)\nend do\nend do\n\nend subroutine faraday_fortran\n')
/usr/local/lib/python3.8/site-packages/IPython/core/interactiveshell.py in run_cell_magic(self, magic_name, line, cell)
2417 with self.builtin_trap:
2418 args = (magic_arg_s, cell)
-> 2419 result = fn(*args, **kwargs)
2420 return result
2421
/usr/local/lib/python3.8/site-packages/decorator.py in fun(*args, **kw)
230 if not kwsyntax:
231 args, kw = fix(args, kw, sig)
--> 232 return caller(func, *(extras + args), **kw)
233 fun.__name__ = func.__name__
234 fun.__doc__ = func.__doc__
/usr/local/lib/python3.8/site-packages/IPython/core/magic.py in <lambda>(f, *a, **k)
185 # but it's overkill for just that one bit of state.
186 def magic_deco(arg):
--> 187 call = lambda f, *a, **k: f(*a, **k)
188
189 if callable(arg):
/usr/local/lib/python3.8/site-packages/fortranmagic.py in fortran(self, line, cell)
377 verbosity=args.verbosity)
378 if res != 0:
--> 379 raise RuntimeError("f2py failed, see output")
380
381 self._code_cache[key] = module_name
RuntimeError: f2py failed, see output
%%fortran
subroutine amperemaxwell_fortran(ex, ey, bz, dx, dy, dt, nx, ny)
implicit none
integer, intent(in):: nx, ny
real(8), intent(in):: dx, dy, dt
real(8), dimension(nx-1, ny-1), intent(inout) :: bz
real(8), dimension(nx-1, ny), intent(inout) :: ex
real(8), dimension(nx, ny-1), intent(inout) :: ey
integer:: i, j
real(8):: dbz_dx, dbz_dy
real(8), parameter:: csq = 1d0
do i = 1, nx-1
dbz_dy = (bz(i, 1)-bz(i, ny-1)) / dy ! periodic BC
ex(i, 1) = ex(i, 1) + dt*csq*dbz_dy
ex(i, ny) = ex(i, 1)
end do
do j = 1, ny-1
dbz_dx = (bz(1,j)-bz(nx-1,j)) / dx ! periodic BC
ey(1,j) = ey(1,j) - dt*csq*dbz_dx
ey(nx,j) = ey(1,j)
end do
do j=2,ny-1
do i=1,nx-1
dbz_dy = (bz(i,j)-bz(i,j-1)) / dy
ex(i,j) = ex(i,j) + dt*csq*dbz_dy
end do
end do
do j=1,ny-1
do i=2,nx-1
dbz_dx = (bz(i,j)-bz(i-1,j)) / dx
ey(i,j) = ey(i,j) - dt*csq*dbz_dx
end do
end do
end subroutine amperemaxwell_fortran
%%time
from tqdm.notebook import tqdm
ex.fill(0.0)
ey.fill(0.0)
hz = - np.cos(m*np.pi*y) * np.cos(n*np.pi*x) * np.cos(omega*(-0.5*dt))
ex = np.asfortranarray(ex)
ey = np.asfortranarray(ey)
hz = np.asfortranarray(hz)
for t in tqdm(range(1000)):
faraday_fortran( ex, ey, hz, dx, dy, dt, nx, ny)
amperemaxwell_fortran(ex, ey, hz, dx, dy, dt, nx, ny)