Maxwell solver in two dimensions with FDTD scheme#

\[ \frac{\partial H_z}{\partial t} = \frac{\partial E_x}{\partial y} - \frac{\partial E_y}{\partial x} ;\qquad \frac{\partial E_x}{\partial t} = \frac{\partial H_z}{\partial y} ;\qquad \frac{\partial E_y}{\partial t} = - \frac{\partial H_z}{\partial x} \]

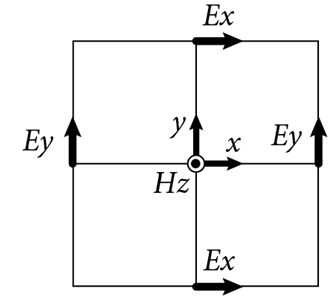fdtd $$ H_z \big|^{n+1/2}{i+1/2,j+1/2} = H_z \big|^{n-1/2}{i+1/2,j+1/2} + \frac{dt}{dy} \big(E_x \big|^{n}{i+1/2,j+1} - E_x \big|^{n}{i+1/2,j} \big)

  • \frac{dt}{dx} \big( E_y \big|^{n}{i+1,j+1/2} - E_y \big|^{n}{i,j+1/2} \big) $$

\[ E_x \big|^{n+1}_{i+1/2,j} = E_x \big|^{n}_{i+1/2,j} + \frac{dt}{dy} \big( H_z \big|^{n+1/2}_{i+1/2,j+1/2} - H_z \big|^{n+1/2}_{i-1/2, j-1/2} \big) \]
\[ E_y \big|^{n+1}_{i,j+1/2} = E_y \big|^{n}_{i,j+1/2} - \frac{dt}{dx} \big( H_z \big|^{n+1/2}_{i+1/2,j+1/2} - H_z \big|^{n+1/2}_{i-1/2, j+1/2} \big) \]

Description of the scheme

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import axes3d
import matplotlib.animation as animation
from IPython.display import HTML

plt.rcParams['figure.figsize'] = (10,6)

# Mesh parameters
nx, ny = 101, 101
vx, dx = np.linspace(0, 1, nx, endpoint=True, retstep=True)
vy, dy = np.linspace(0, 1, ny, endpoint=True, retstep=True)

#Initialize Ex, Ey when time = 0
ex = np.zeros((nx-1, ny), dtype=np.double)  
ey = np.zeros((nx, ny-1), dtype=np.double) 
nbiter = 500   # time loop size
dt = 0.001     # time step
m, n = 2, 2
omega = np.sqrt((m*np.pi)**2+(n*np.pi)**2)
# Create the staggered grid for Bz
x, y = np.meshgrid(0.5*(vx[:-1]+vx[1:]), 0.5*(vy[:-1]+vy[1:]))

fig = plt.figure()
ax = axes3d.Axes3D(fig)

#Initialize Bz when time = - dt / 2
hz = - np.cos(m*np.pi*y) * np.cos(n*np.pi*x) * np.cos(omega*(-0.5*dt))
wframe = ax.plot_wireframe(x, y, hz, rstride=2, cstride=2)
ax.set_zlim(-1,1);

<Figure size 1000x600 with 0 Axes>

numpy#

def faraday( ex, ey, hz ) : 
    "faraday equation Bz(t+dt/2) -> Bz(t-dt/2) + dt f(E(t))"
    return hz + dt * ((ex[:, 1:]-ex[:, :-1]) / dy - (ey[1:, :]-ey[:-1, :]) / dx)

def ampere_maxwell( hz, ex, ey):
    " Ampere-Maxwell equation E(t+dt) -> E(t) + dt g(Bz(t+dt/2)) "
    ex[:, 1:-1] += dt*(hz[:, 1:]-hz[:, :-1]) / dy
    ey[1:-1, :] += - dt*(hz[1:, :]-hz[:-1, :]) / dx

    # periodic boundary conditions
    ex[:, 0] += dt*(hz[:, 0]-hz[:, -1]) / dy
    ex[:, -1] = ex[:, 0]
    ey[0, :] += - dt*(hz[0, :]-hz[-1, :]) / dx
    ey[-1, :] = ey[0, :]
    
    return ex, ey

def update(i, ax, fig):
    ax.cla()

    global ex, ey, hz

    hz = faraday( ex, ey, hz)
    ex, ey = ampere_maxwell( hz, ex, ey)
    
    wframe = ax.plot_wireframe(x, y, hz, rstride=2, cstride=2)
    ax.set_zlim(-1, 1)
    return wframe,

ani = animation.FuncAnimation(fig, update,
                              frames=range(200),
                              fargs=(ax, fig), interval=100)

%%time
HTML(ani.to_html5_video())

CPU times: user 3.53 s, sys: 184 ms, total: 3.72 s
Wall time: 4.42 s

%%time

from tqdm.notebook import tqdm

nx, ny = 512, 512
vx, dx = np.linspace(0, 1, nx, endpoint=True, retstep=True)
vy, dy = np.linspace(0, 1, ny, endpoint=True, retstep=True)

ex = np.zeros((nx-1, ny), dtype=np.double)  
ey = np.zeros((nx, ny-1), dtype=np.double) 
dt = 0.001     # time step
m, n = 2, 2
omega = np.sqrt((m*np.pi)**2+(n*np.pi)**2)
x, y = np.meshgrid(0.5*(vx[:-1]+vx[1:]), 0.5*(vy[:-1]+vy[1:]))

hz = - np.cos(m*np.pi*y) * np.cos(n*np.pi*x) * np.cos(omega*(-0.5*dt))

for t in tqdm(range(1000)):
    
    hz = faraday( ex, ey, hz)
    ex, ey = ampere_maxwell( hz, ex, ey)
    

CPU times: user 3.15 s, sys: 601 ms, total: 3.75 s
Wall time: 3.74 s

%load_ext fortranmagic

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
Cell In[9], line 1
----> 1 get_ipython().run_line_magic('load_ext', 'fortranmagic')

File /usr/share/miniconda3/envs/runenv/lib/python3.10/site-packages/IPython/core/interactiveshell.py:2369, in InteractiveShell.run_line_magic(self, magic_name, line, _stack_depth)
   2367     kwargs['local_ns'] = self.get_local_scope(stack_depth)
   2368 with self.builtin_trap:
-> 2369     result = fn(*args, **kwargs)
   2370 return result

File /usr/share/miniconda3/envs/runenv/lib/python3.10/site-packages/IPython/core/magics/extension.py:33, in ExtensionMagics.load_ext(self, module_str)
     31 if not module_str:
     32     raise UsageError('Missing module name.')
---> 33 res = self.shell.extension_manager.load_extension(module_str)
     35 if res == 'already loaded':
     36     print("The %s extension is already loaded. To reload it, use:" % module_str)

File /usr/share/miniconda3/envs/runenv/lib/python3.10/site-packages/IPython/core/extensions.py:76, in ExtensionManager.load_extension(self, module_str)
     69 """Load an IPython extension by its module name.
     70 
     71 Returns the string "already loaded" if the extension is already loaded,
     72 "no load function" if the module doesn't have a load_ipython_extension
     73 function, or None if it succeeded.
     74 """
     75 try:
---> 76     return self._load_extension(module_str)
     77 except ModuleNotFoundError:
     78     if module_str in BUILTINS_EXTS:

File /usr/share/miniconda3/envs/runenv/lib/python3.10/site-packages/IPython/core/extensions.py:91, in ExtensionManager._load_extension(self, module_str)
     89 with self.shell.builtin_trap:
     90     if module_str not in sys.modules:
---> 91         mod = import_module(module_str)
     92     mod = sys.modules[module_str]
     93     if self._call_load_ipython_extension(mod):

File /usr/share/miniconda3/envs/runenv/lib/python3.10/importlib/__init__.py:126, in import_module(name, package)
    124             break
    125         level += 1
--> 126 return _bootstrap._gcd_import(name[level:], package, level)

File <frozen importlib._bootstrap>:1050, in _gcd_import(name, package, level)

File <frozen importlib._bootstrap>:1027, in _find_and_load(name, import_)

File <frozen importlib._bootstrap>:1006, in _find_and_load_unlocked(name, import_)

File <frozen importlib._bootstrap>:688, in _load_unlocked(spec)

File <frozen importlib._bootstrap_external>:883, in exec_module(self, module)

File <frozen importlib._bootstrap>:241, in _call_with_frames_removed(f, *args, **kwds)

File /usr/share/miniconda3/envs/runenv/lib/python3.10/site-packages/fortranmagic.py:36
     34 from IPython.utils import py3compat
     35 from IPython.utils.io import capture_output
---> 36 from IPython.utils.path import get_ipython_cache_dir
     37 import numpy as np
     38 from numpy.f2py import f2py2e

ImportError: cannot import name 'get_ipython_cache_dir' from 'IPython.utils.path' (/usr/share/miniconda3/envs/runenv/lib/python3.10/site-packages/IPython/utils/path.py)

fortran#

%%fortran 

subroutine faraday_fortran( ex, ey, bz, dx, dy, dt, nx, ny)
implicit none

real(8), intent(in) :: ex(nx-1,ny)
real(8), intent(in) :: ey(nx,ny-1)
real(8), intent(inout) :: bz(nx-1,ny-1)
integer, intent(in) :: nx, ny
real(8), intent(in) :: dx, dy, dt

integer :: i, j
real(8) :: dex_dx, dey_dy
real(8) :: dex_dy, dey_dx
        
do j=1,ny-1
do i=1,nx-1
   dex_dy  = (ex(i,j+1)-ex(i,j)) / dy
   dey_dx  = (ey(i+1,j)-ey(i,j)) / dx
   bz(i,j) = bz(i,j) +  dt * (dex_dy - dey_dx)
end do
end do

end subroutine faraday_fortran

%%fortran

subroutine amperemaxwell_fortran(ex, ey, bz, dx, dy, dt, nx, ny)

    implicit none
    integer, intent(in):: nx, ny
    real(8), intent(in):: dx, dy, dt
    real(8), dimension(nx-1, ny-1), intent(inout) :: bz
    real(8), dimension(nx-1, ny),   intent(inout) :: ex
    real(8), dimension(nx, ny-1),   intent(inout) :: ey
    integer:: i, j
    real(8):: dbz_dx, dbz_dy
    real(8), parameter:: csq = 1d0
    
    do i = 1, nx-1
       dbz_dy = (bz(i, 1)-bz(i, ny-1)) / dy ! periodic BC
       ex(i, 1) = ex(i, 1) + dt*csq*dbz_dy
       ex(i, ny) = ex(i, 1)
    end do
    
    do j = 1, ny-1
       dbz_dx = (bz(1,j)-bz(nx-1,j)) / dx  ! periodic BC
       ey(1,j) = ey(1,j) - dt*csq*dbz_dx
       ey(nx,j) = ey(1,j)
    end do
    
    do j=2,ny-1
        do i=1,nx-1
           dbz_dy = (bz(i,j)-bz(i,j-1)) / dy
           ex(i,j) = ex(i,j) + dt*csq*dbz_dy 
        end do
    end do
    
    do j=1,ny-1
        do i=2,nx-1
           dbz_dx = (bz(i,j)-bz(i-1,j)) / dx
           ey(i,j) = ey(i,j) - dt*csq*dbz_dx 
        end do
    end do

end subroutine amperemaxwell_fortran

%%time

from tqdm.notebook import tqdm

ex.fill(0.0)
ey.fill(0.0)
hz = - np.cos(m*np.pi*y) * np.cos(n*np.pi*x) * np.cos(omega*(-0.5*dt))
ex = np.asfortranarray(ex)
ey = np.asfortranarray(ey)
hz = np.asfortranarray(hz)

for t in tqdm(range(1000)):
    
    faraday_fortran( ex, ey, hz, dx, dy, dt, nx, ny)
    amperemaxwell_fortran(ex, ey, hz, dx, dy, dt, nx, ny)